October 2016 – Page 3 – Cross adaptive processing as musical intervention

As mentioned in the rhythm analysis part 1 , one of our goals at this point has been to try to find methods of rhythmical analysis that work without assumptions about pulse and meter, and also as far as possible without assumptions about musical style. As our somewhat minimal rhythm definition we look at rhythm as time ratio constellations , patterns of time ratios . Here we will make an assumption (yes, something must be assumed) regarding patterns of time durations: Recurring or repeated patterns have another perceptual quality than constantly shifting combinations of time durations. We could also assume that recurring or repeated patterns have stronger perceptual influence, but technically, it does not matter so much. The main issue is that we can measure some difference in quality. Quality here does not imply that something is better, just that something is different.

FFT of modified amplitude envelope

To measure how much recurrence there is in a signal, we can use autocorrelation. Repeated patterns will show up as peaks in the autocorrelation, and the period of repetition will be shown as the position of the peaks. Longer repetition periods give peaks further away (commonly further to the right when graphing the autocorrelation). To calculate the autocorrelation, we could use the FFT of the amplitude envelope as our basis. However, the unmodified envelope can have many variations at frequencies not related to the actual rhythms. For example, the amplitude envelope of a signal with fast transients (e.g. percussion, piano) show much more high frequency content than a signal with slow transients (e.g. many wind instruments). For this reason, we opted to use a modified envelope for the FFT in connection with the rhythm autocorrelation measure. The modified envelope is generated by using transient detection, triggering a short gaussian envelope scaled to the current amplitude of the signal. This way, we achieve a consistent envelope across different instruments, preserving the relative amplitude differences between transients (since we assume dynamics to be relevant to rhythm, for example in using accents to signify grouping of events).

Time spans and latency

One question to ask when analyzing for recurring patterns is “how long patterns are we looking for?” . One could say that a musical pattern sometimes will repeat relatively quickly, say once every second. Other times we can have arbitrary long patterns (sometimes very long), but for practical purposes, lets assume a maximum length of somewhere around 10 seconds. Now, if we want to analyze for such long patterns (10 seconds), an inherent limitation of any technique used would imply that it takes at least so many seconds to give an answer to whether there is a repeating pattern of that duration. Analyzing for 1-second patterns, we can have an indication after 1 second, and we can be sure after 2 seconds. For a musically responsive analysis, we’d like as low latency as possible, and in any practical case a latency of 10 seconds or more is not particularly responsive. Still, if the analysis window is shorter, we will not be able to detect longer patterns. One common method in FFT is to use overlapping windows, meaning that we update our analysis several times (with new data) within the time span defined by one analysis window. This will give us updated data more frequently, but still the longer patterns will only partially be influencing the output until a full period has passed. To alleviate this, we used 3 analysis durations running in parallel layers (each with overlapping windows as previously described). The longest time span is set to 10 seconds, layered onto this is a time span of 5 seconds, and layered on top of this again a 2.5 second time span. The layers are mixed down using a weighted sum that give precedence to more recent data while retaining the larger time span context. The shortest time span layer will be updated twice as often as the medium time span layer, and this again is updated twice as often as the longest time span layer. When we have a new frame of the longer time span, we will also have a new frame of the short time span ,these are then weighted 2/3 and 1/3 respectively. At the next available frame for the shorter time span, we weigh the new frame 2/3, and the longer frame 1/3. This is combined similarly for all the 3 layers to form the final autocorrelation coefficients. These are shown as a graph in the GUI.

rhythmcorrgraph1 — 3-layer rhythm autocorrelation. The red line is the shortest FFT, Light blue is the medium, Green is the longest. Yellow line is the weighted sum. This figures shows a steady rhythm played statically over the full duration of the longest FFT layer (10 seconds).

rhythmcorrgraph2 — 3 layer rhythm autocorrelation, as above. Here we see the recently played faster rhythms, with the long time span showing the static slower pulse. The combined correlation (yellow) has both features.

rhythmcorrgraph3 — 3 layer rhythm autocorrelation, as above. Showing a more randomly spaced non-repeating rhythm.

rhythmcorrgraph4 — As above. Recently played steady fast rhythms after a period of randomly spaced non-repeating activity

Features under development

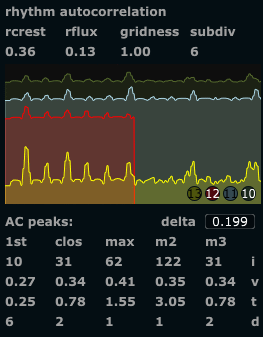
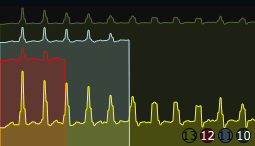
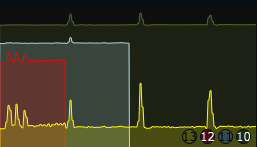
We have assumed that we could use the exact position of the peaks to detect the duration of repeated patterns . This is partly true, since fast rhythms (short repetition duration) give tightly spaced peaks, slow rhythms give sparsely spaced peaks. It seems so far, however, that the exact position and amplitude of each peak is not really stable enough to just use these values for that purpose. We use a peak picking algorithm to detect the highest peak, the second and third highest peak, and also the peak closest in time to the maximum peak and the first (earliest, leftmost) peak. In situations where the rhythm is quite static, these values correspond well to the repetition durations and the relative strength (in dynamics) of different repeating patterns. For most practical situations however, this specific application of the rhythmic autocorrelation does not really work that well (yet!). Another way of using these values could be to determine the degree to which the rhythmic events can be placed on a grid. We have termed this gridness . It is calculated by taking the maximum peak as the reference duration, then looking at the other detected peaks, and checking if we can find some relatively simple integer ratio between the max and each other peak. For example, if we have a max peak at 6 seconds, and then a second highest peak at 4 seconds, the ratio would be 3:2. In this case we construct a grid of 1/3 durations of the max peak across the whole time segment (1/3, 2/3, 3/3, 4/3, 5/3 … and so on as far as we can go), and see how many of all detected peaks correspond to grid locations. The process is repeated for each integer ratio found between the max peak and the lesser peaks. The grid with the maximum number of corresponding events wins, and is reported as the current rhythmic subdivision . The number of peaks that fall on this grid is divided by the number of detected events, resulting in the gridness value. If all detected events fall on grid locations, the gridness will be 1.0, if half of the events fall on the grid the gridness will be 0.5. The gridness measure does not currently work very well, due to the instability of the peaks as described above. This is an area of the analyzer where substantial refinement can take place. The resulting metrics (if working) however, seems intuitively to make sense; Measuring periods of repetition, subdivisions of these, and the degree of consistence with the assumed grid of subdivisions.

So what can we actually use it for now?

Following up on a suggestion from Miller Puckette, we tried to look at more general features of the correlation graph, to extract some global descriptors of the current rhythmic activity. We turned to well known statistics like crest and flux .
The crest factor describing how “peaky” the signal is, that is the relation between the highest peak and the overall effective amplitude. Traditionally the crest would be calculated as the peak value divided by the rms (root-mean-square) amplitude. However, our use here is somewhat different than both the regular envelope crest and the spectral crest. For this specific purpose, we found it better to divide the rms value by the number of transients detected. This may at first seem counterintuitive, but can be explained by the fact that repeated patterns of the same duration creates many events that fall on the same peak locations in the autocorrelation, effectively making those peaks stronger. The division on the number of peaks detected avoids the exessively high crest values we could get if there was a single peak in the correlation. As such it gives a measure of the amount of repetition. It could be discussed whether we should use another term for this feature, to avoid confusion between this and the other creest measures.
The flux generally describes the amount of change from frame to frame, so static patterns will have low flux while constantly shifting rhythms will have high flux. The flux is calculated similarly as it would be for spectral flux (multiplying each value in a frame with the corrresponding value in the previous frame, accumulating the result and then normalizing it). This is done with a slight twist in our implementation; Because of the instability in the peaks’ location we don’t just multiply each value with the corresponding value of another frame, but we check if any neightbouring values have higher amplitude, and then use the maximum (this value or its neighbour on either side). We can think of this as the minimum possible flux. Empirical testing has shown it to be a more stable measure than the simpler variation of the flux measure.

rhythmautocorr_full — All results related to the rhythmic autocorrelation. The crest and flux are relatively reliable measures. The other ones subject to refinement. Note that the AC peaks in the lower half of the figure currently refers only to the long time span (green) autocorrelation.

The first instances of the MIDIator could sum two analysis signals, with separate scaling and sign inversion for each one. Recently, we’ve added two new methods for mixing those two signals, so it warrants this post to explain how it works and which problems it is intended to solve.

For all mix methods there is a MIDI output configuration to the right. All modules output MIDI controller values. We can set the MIDI channel and controller number, enable/disable the module, and also enter notes about the mapping/use of the module. Notes will be saved with the project.

Do take care however, for your own records, take a screenshot of your settings and save this with your project. The plugins can and will change during the further development of the project. If this leads to changes in the GUI configuration (i.e. the number of user interface elements) changes, there is a high probability that not everything will be recalled correctly. In that case you must reconstruct your settings from the (previously saved) screenshot.

Add

Each of the two signals have separate filtering, with separate setting for the rise and fall times. The two signals are scaled (with scale range being from -1 to + 1), and then added together. If both signals are scaled positively, each of them affects the output positively. If one is scaled negatively and the other positively, more complex interactions between them will form. For example, with rms (amplitude) being scaled negatively while transient density is scaled positively; the output will increase with high transient density, but only if we are not playing loud.

midiator_add — Example of the “add” mix method. Higher amplitude (rms) will decrease the output, while higher transient density will increase the output. This means that soft fast playing will produce the highest possible output with these settings.

Abs_diff

This somewhat cryptic term refers to the absolute difference between two signals. We can use it to create an interaction model between two signals, where the output goes high only if the two analysis signals are very diffferent . For example, if we analyze amplitude (rms) from two different musicians, the resulting signal will be low as long as they both play in the same dynamic register. If one plays loud while the other plays soft, the output will be high, regardless of which of the two plays loud. It could also of course be applied to two different analysis signals from the same musician, for example the difference between pitch and the spectral centroid.

Gate

The gate mixmethod can be used to turn things on or off. It can also be used to enable/disable the processing of another MIDIator module, effectively acting as a sample and hold gate. The two input channels now are used for different purposes: one channel turns the gate on , the other channel turns the trigger off . Each channel has a separate activation threshold (and selection if the signal must pass the threshold moving upwards or downwards to activate). For simple purposes, this can act like a Schmitt trigger , also termed hysteresis in some applications. This can be used to reduce jitter noise in the output, since the activation and deactivation thresholds can be different.

It can also be used to create more untraditional gates. A simple variation let us create a gate that is activated only if the input signal is within a specified band. To do this, the activation threshold must be lower than the deactivation threshold, like this:

midiator_gate_same_band — Band-activated gate. The gate will be activated once the signal crosses the (low) activation threshold. Then it will be turned off once the signal crosses the (higher) deactivation threshold in an upward direction. To activate again, the signal must go lower than the activation threshold.

The up/down triggers can be adjusted to fine tune how the gate responds to the input signal. For example, looking at the band-activated gate above: If we change the deactivation trigger to “down”, then the gate will only turn off after the signal has been higher than the deactivation threshold and then is moving downwards .

So far, we’ve only looked at examples where the two input signals to the gate is the same signal. Since the two input signals can be diffeerent (even come from two different acoustic source, highly intricate gate behaviour can be constructed. Even though the conception of such signal-interdependent gates can be complex (inventing which signals could interact in a meaningful way), the actual operation of the gate is technically no different. Just for the case of the example, here’s a gate that will turn on if the transient density goes high, then it will turn off when the pitch goes high. To activate the gate again, the transient density must first go low , then high .

midiator_gate_different — Gate with different activation and deactivation signals. Transient density will activate the gate, while pitch will deactivate it.

Sample and hold:

The gate mixmethod also can affect the operation of another MIDIator module. is currently hardcoded, so that it will only affect the next module (the one right below the gate). This means that, when the gate is on, the next MIDIator module will work as normal, but when the gate is turned off it will retain the value it has reached at the moment the gate is turned off. In traditional signal processing terms: sample and hold . To enable this function, turn on the button labeled “s/h”.

midiator_gate_sh — The topmost of these two modules agt as a sample and hold gate for the lower module. The lower module mapping amplitude to positively affect the output value, but is only enabled when the topmost gate is activated. The situation in the figure shows the gate enabled.

Month: October 2016

Rhythm analysis, part 2